Assessing the Dynamicist's Challenge in Cognitive Science
Cognitive Science, 22, 295-318
William Bechtel
Philosophy-Neuroscience-Psychology Program
Department of Philosophy
Washington University in St. Louis
Abstract
Advocates of dynamical systems theory (DST) sometimes employ revolutionary rhetoric. In an attempt to clarify how DST models differ from others in cognitive science, I focus on two issues raised by DST: the role for representations in mental models and the conception of explanation invoked. Two features of representations are their role in standing-in for features external to the system and their format. DST advocates sometimes claim to have repudiated the need for stand-ins in DST models, but I argue that they are mistaken. Nonetheless, DST does offer new ideas as to the format of representations employed in cognitive systems. With respect to explanation, I argue that some DST models are better seen as conforming to the covering-law conception of explanation than to the mechanistic conception of explanation implicit in most cognitive science research. But even here, I argue, DST models are a valuable complement to more mechanistic cognitive explanations.
1. Introduction
Dynamical systems theory (DST) is changing the manner in which many cognitive scientists think about cognition. It provides a new set of tools to use in trying to understand how the mind-brain carries out cognitive tasks. In particular, it offers a much expanded conception of computation and important conceptual tools, such as the concept of an "attractor," for understanding activity in complex systems. Moreover, since dynamical systems can couple with other dynamical systems, the DST approach provides a way to overcome the separation, which has been prevalent in both experimental research in cognitive psychology and modeling work in AI, between mind/brain and the world. Indeed, coupled systems can be reconceived as one system; when applied to the mind-brain and the world, this leads to a fundamental integration of mind and world. As Andy Clark (1996) argues, drawing on numerous research projects of DST theorists, much of what we take to be cognitive activity depends upon the way we coordinate our activities with features of the world. Hence, he suggests that the mind may not be fully contained in the brain, but "leaks" out into the world.
While the DST approach certainly expands the conceptual tools for thinking about cognitive phenomena, many proponents want to claim much more; they often portray it as constituting a revolution. van Gelder and Port make this clear in the introduction to their important collection of recent DST work related to mental life, Mind as Motion. They explicitly draw upon Kuhn's notion of a paradigm and of paradigm change in describing DST:
The claim to be offering a different paradigm or worldview should raise some fundamental questions for all cognitive scientists: Is the dynamicist worldview compatible with other worldviews in cognitive science? The passages from van Gelder and Port suggest that it is not, but they may be wrong. Whether compatible or not, a more fundamental question is: in what respects does DST differ from other viewpoints in cognitive science? In addressing this question, I shall focus on two features of van Gelder and Port's conception of the DST worldview: (1) its repudiation of representations and (2) its conception of explanation. I shall argue that despite the frequent focus on representations as the point of demarcation, the greater difference between some DST research and most other approaches to cognitive science involves the conception of explanation. Even here, though, I will argue that, while different, the model of explanation employed in many DST models is compatible with the more common conception of explanation in cognitive science, and may offer an important supplement to it.
2. Two Aspects of Representation
A major target in the dynamicists' claim to be advancing a new paradigm is their abandonment of "sophisticated internal representations" (van Gelder, 1995, p. 346). From what I have already said about the potential of the DST approach to integrate the mental system and the world, the attack on representations is quite intelligible. As we shall soon discuss, one of the functions of representations is to stand in for things outside the system; once a system has representations, it can operate on them and not need the world (Fodor, 1980). Getting rid of representations thus facilitates reconnecting cognition and the world.
The term "representation" is used in a variety of different ways in cognitive science, making it challenging to assess the different claims different cognitive scientists make about representations. To provide a basis for evaluating the DST challenge to representations, it is useful to begin with by distinguishing two aspects of representations, the function of a representation as standing in for something else, and the format employed in the representation. In terms of it, we can then assess the DST challenge to representations.
2.1 Representations as stand-ins
The most common route for introducing representations into cognitivist theorizing begins by construing the mind/brain as involved in coordinating the behavior of an organism in its environment. A major strategy in cognitive science has been to explain how such an organism is successful in negotiating its environment by construing some of its internal states or processes as carrying information about, and so standing in for, those aspects of its body and external states or events that it takes account of in negotiating its environment. (This does not require assuming that the mind builds up a complete model of its body and environment; rather, a stand in is needed only for those aspects that are relevant for guiding behavior. See Ballard, 1991, and Churchland, Ramachandran, and Sejnowski, 1994.)
It is this notion of standing-in which Newell and Simon emphasize in their characterization of a symbol: "The most fundamental concept for a symbol system is that which gives symbols their symbolic character, i.e., which lets them stand for some entity. We call this concept designation, though we might have used any of several other terms, e.g., reference, denotation, naming, standing for, aboutness, or even symbolization or meaning" (Newell, 1980, p. 156). Newell goes on to offer a definition of designation:
While there is a good deal of agreement about the importance of the standing-in aspect of representations, it is considerably more difficult to explicate what it is for one thing to stand in for another. Philosophers who have tried to explicate this notion have looked in two different directions: back to the object or event for which the object is to stand in and forward to the process which will use the representation in leu of that for which it stands in.
Philosophers such as Dretske have grounded their account of the relation between representations and the represented objects or events in the notion of information: the representation carries information about the objects or events represented. They have further explicated the notion of information in terms of reliable covariation, usually mediated by causal relationships. Mercury thermometers, for example, carry information about temperature due to the causal processes that result in a reliable covariation between the height of a mercury column and temperature.
Most theorists recognize, however, that reliable covariation is not sufficient to establish something as a representation, as opposed to being a natural sign (Hatfield, 1990) or index (Dretske, 1988). For one thing, it seems an essential aspect of representation that misrepresentation is possible. The additional component on which theorists generally insist is that a representation has as its function the carrying of specific information, where the notion of function is explicated in teleological terms via evolutionary theory. Something has a function, in such analyses, when its current existence is explained in terms of selection processes (biological or social) that operated on it (Wimsatt, 1972). To identify the selection process and thus the function of an information-bearing state or process, one must focus on the user of the information: if there is another process which regularly employs the state or process in virtue of the information in bears to accomplish its function, then the state or process is a representation (Dretske, 1988; Hatfield, 1990). When the state or process arises without carrying the information for which it was selected, then misrepresentation occurs.
In this analysis, it might seem that a representation must generally be a reliable indicator of that which it represents. But Millikan (1984, 1993) argues that something could have a function even if only rarely do things of that type succeed in performing that function (e.g., most sperm do not succeed in fertilizing eggs). Applied to representations, she argues that something could be a representation even if it rarely or never actually carries information (that is, actually covaries with that about which it represents). For example, we might design an instrument to detect radiation leaks, and even if it never actually produced anything but false alarms (since there never was a radiation leak), its alarms would still represent radiation leaks. According to Millikan, therefore, what makes something a stand in for something else is that it functions that way for some processing system, not that it carries information about it.
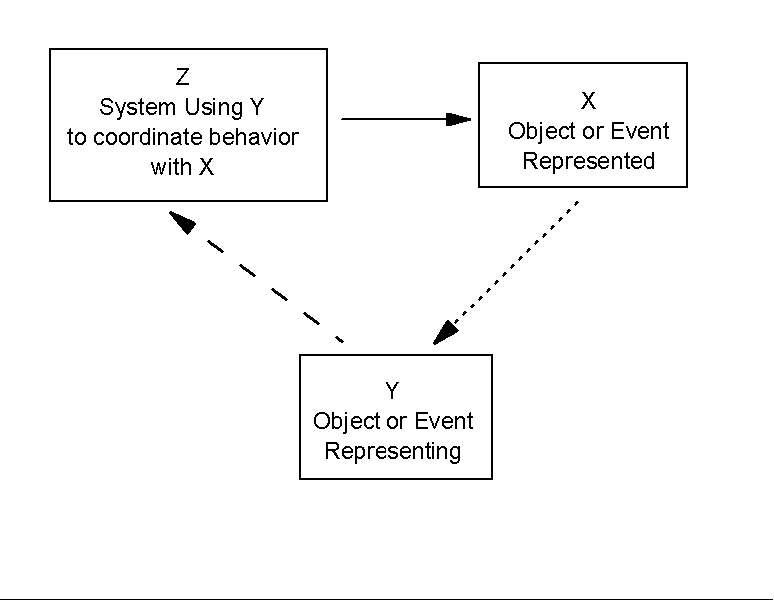
Since Millikan seems right in contending that something could be a representation even if never covarying with that for which it stands in, it is the function of a representation for a user that ultimately determines whether something does stand in for something else. In practice, however, covariation is often a primary tool in discovering what serves as a representation. Thus, in Lettvin et al's (1959) classic study, it was the fact that the firing rate of cells in the frog's retina increased in response to small, blob-like shapes moving across their receptive field that researchers construed them as bug detectors. Functional considerations (e.g., that the frog responds to increased firing in these retinal cells as would be appropriate for catching bugs) enter in determining that these are bug detectors, not small-moving-blob detectors. There are, therefore, three interrelated components in a representational story: what is represented, the representation, and the user of the representation (Figure 1).

Figure 1. Three components in an analysis of representation: the representation
Y carries information about X for Z, which uses Y in order to act or think
about X.
2.2 The format of representations
In fleshing out what it is for a representation to stand in for something else, I have already emphasized the process in which it is used. In order for a process to use a representation, the process must be coordinated with the format of the representation. In classical computer models, the format of the representation has to be appropriate for the processes that operate upon it. In connectionist and neuroscience models one generally does not think of processes operating on representations, but of states produced within the processing system constituting representations insofar as they are stand-ins in the causal process. Nonetheless, there is still the need for a coordination between the format of the representation and the process. Only states appropriate to the process will count as representations.
One might try to defuse the distinction just made between processes operating on representations and representations figuring in processes by noting that one can look at traditional AI programs as well as connectionist networks and brains as carrying out overall processes. It is in the service of our efforts to understand the overall process that we try to identify representations that figure in it. But there is a point to emphasizing the difference between processes operating on representations and representations figuring in processes when considering DST. It is the former locution that supports the construal of representations as static entities sitting in memory until an operation is performed on them. When representations are identified in processes, then it is possible for them to change dynamically. Once this is recognized, however, it also becomes clear that not all traditional AI programs construe representations as static except when operated on by rules. Spreading activation models (Anderson, 1983, 1990), for example, allow for dynamic processes to change at least the activation of representations independently of rules such as production system rules that might operate on them.
Many of the acrimonious disputes in cognitive science have focused on the format of representations. The battle over mental imagery was largely a battle over whether the processes in which mental images are used requires a depictive representational format (Kosslyn, 1980, 1994), or can be accommodated by a propositional format (Pylyshyn, 1971, 1981). Likewise, some of the conflicts over connectionism have focused on the adequacy of the representations used in connectionist networks. Fodor and Pylyshyn, for example, (1988) argue that mental representations must be compositional in order for cognitive agents to be productive and systematic in their behavior. Connectionists have advanced numerous responses to Fodor and Pylyshyn. van Gelder (1990), for example, drawing upon work of Smolensky (1990) and Pollack (1990), has argued that connectionist representations which are only implicitly rather than explicitly compositional might be sufficient to secure the advantages of compositional structure.
One side in both of the disputes noted in the previous paragraph have drawn their model for representation from natural languages. Indeed, propositions, as found either in natural languages or symbolic logic, have had a powerful influence in some cognitive scientists' thinking about the format of representations. Even those who have employed symbolic representations have often employed them in more complex ways, utilizing for example structures such as scripts (Schank and Abelson, 1977) and frames (Minsky, 1975). Connectionists have adopted a different approach. Rather than designing rules to work on representations, most connectionists have designed networks to transform input representations into output representations. They then appeal to representations both in characterizing the inputs and outputs of these networks and in analyzing what is happening within the networks themselves. In the latter task, one can focus on either the weights on the connections (constituting the latent knowledge of the system) or the patterns of activation on the hidden units (constituting the occurrent activities of the system). Both have been characterized as constituting representations and a number of connectionists have tried to figure out the content of these representations (e.g., using cluster analysis or principal components analysis to analyze the patterns produced on hidden units as in Elman, 1991).
The point to be emphasized here is that cognitive scientists have explored a wide variety of representational formats, some utilizing a propositional format that draws its initial inspiration from natural languages, and some repudiating it. Indeed, one might identify variation in the format of representations used as one of the major points of difference in cognitive science research.
3. The DST Challenge to Representations
With this distinction between the stand-in and format aspects of representations and a brief characterization of how they have figured in cognitive science, we can turn now to the DST challenge to representations. What makes the DST challenge a particular strong one is that it is directed at both the stand-in and format aspects of representations. The challenge to the stand-in feature of representations is found most clearly in van Gelder (1995) analysis of Watt's centrifugal governor for the steam engine, which he offers as a prototype or exemplar of a dynamical system and as a "landmark for models of cognition" (p. 381).
The governor was designed by Watt to solve the problem of maintaining constant speed for the flywheel of a steam engine. Watt solved this problem by a technology already employed in windmills. It involved attaching a vertical spindle to the flywheel which would rotate at a speed proportionate to the speed of the flywheel. He attached two arms with metal balls on their ends to the spindle; these arms were free to rise and fall and, due to centrifugal force, would do so in proportion to the speed of the governor. Through a mechanical linkage, the angle of the arms would change the opening of a valve, thereby controlling the amount of steam driving the flywheel. This provided a system in which, if the flywheel was turning too fast, the arms would rise, causing the valve to partly close. This would reduce the amount of steam available to turn the flywheel, thereby slowing it down. On the other hand, if the flywheel was turning too slowly, the arms would drop and this would cause the valve to open, resulting in more steam and hence an increase in the speed of the flywheel (Figure 2a).
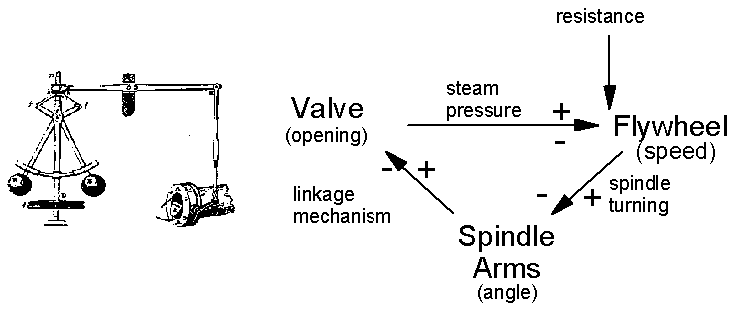
Figure 2. Watt's centrifugal governor for a steam engine. (a) Drawing from J. Farley, A Treatise on the Steam Engine: Historical, Practical, and Descriptive (London: Longman, Rees, Orme, Brown, and Green, 1927). (b) A schematic representation in the same format as Figure 1, showing that the angle of the Spindle Arms carries information about the speed of the Flywheel for the Valve, which uses the angle to determine the opening, thereby regulating the speed of the Flywheel.
As a first step toward establishing that cognitive systems, construed as dynamical systems, lack representations, van Gelder argues that the Watt governor operates without representations. He calls "misleading" "a common and initially quite attractive intuition to the effect that the angle at which the arms are swinging is a representation of the current speed of the engine, and that it is because the arms are related in this way to engine speed that the governor is able to control that speed" (p. 351). What is at stake here is whether the angle of the arms is a stand in for the current speed of the engine. (Recall that in the passage cited earlier, van Gelder does accept the view that basic to being a representation is standing in for the thing represented.) Even though the Watt governor is not a particularly interesting case of a representational system, I nonetheless contend that the arm angles do meet the conditions set out above for being a stand in, and so satisfying that aspect of a representation.
I will develop my argument that the arm angle constitutes a representation of the speed of the flywheel by responding to several of van Gelder's arguments to the contrary in turn. His first argument is key: van Gelder contends that for something to be a representation, there ought to be some "explanatory utility in describing the system in representational terms" and he contends that there is no explanatory utility in this case. He states: "A noteworthy fact about standard explanations of how the centrifugal governor works is, however, that they never talk about representations" (van Gelder, 1995, p. 352). The relevance of this observation is questionable. We are not concerned with whether the term "representation" is used but rather whether the explanation of the operation of the Watt governor identifies states which stand in for other states and indeed are used by a system because they so stand in. van Gelder's own explanation of the operation of the governor clearly appeals to the angle of the arms standing in for the speed of the flywheel, and it being used by the component which opens and closes the valve: "the result was that as the speed of the main wheel increased, the arms raised, closing the valve and restricting the flow of steam; as the speed decreased, the arms fell, opening the valve and allowing more steam to flow." The spindle arms clearly intercede between the flywheel and the valve causally and noting this causal relation is a starting point. For us to understand why this mechanism works, though, it is crucial that we understand the angle of the spindle arms as standing in for the speed of the flywheel.
This point can perhaps be made clearer by recognizing that the Watt governor consists of three separate components, each of which operates on different engineering principles (see figure 2b). The opening of the steam value determines the steam pressure. It is this, together with the resistance resulting from the work being done by the engine, which determines the speed at which the flywheel turns. The physical principles at work here are ones of steam pressure and mechanical resistance. The flywheel is linked to the spindle arm mechanism by the spindle; it is the spindle speed which determines, via centrifugal force, the arm angle. Finally, the arm angle determines the valve opening through principles of mechanical linkage. Once we separate the three components and recognize that they work by different principles, we can recognize how the angle of the spindle arms relates to the other two components. It is because the spindle arms rise and fall in response to the speed of the flywheel that the angle of the arms can be used by the linkage mechanism to open and shut the valve. The fact that the angle of the spindle arms represents the speed of the flywheel becomes more clear when we consider why it was inserted into the mechanism to begin with. The flywheel itself has a speed, but there is no way to use this directly to open and close the valve. The spindle and arms were inserted so as to encode information about the speed in a format that could be used by the valve opening mechanism. The reason no one has to comment explicitly on the fact that the arm angles stand in for and thus represent the speed of the flywheel is that this system is very simple, and most people see the connection directly. But if someone does not understand how the governor works, the first thing one would draw attention to is how the spindle arm angle registers the speed of the flywheel.
van Gelder also offers three other arguments against interpreting the angle of the spindle arms as a representation. In the first he grants what he takes to be a necessary assumption for a representational account, namely, that the arm angle correlates with the flywheel speed. He then argues that mere correlation between two items is not sufficient for one to represent the other. In the analysis presented above, however, we explicitly granted that correlation was not sufficient for representation, and emphasized the importance of the user of the representation. In this case, Watt devised the whole device so that the steam valve could use the information encoded in the arm angles as an indicator of the speed of the flywheel.
van Gelder's next move is to reject the just granted assumption and deny that there is even a correlation between the arm angle and the flywheel speed. Without a correlation, he contends, there is no representation: "to talk of some kind of correlation between arm angle and engine speed is grossly inadequate, and once this is properly understood, there is simply no incentive to search for this extra ingredient [i.e. a representation]." (van Gelder, 1995, p. 352). The reason that correlation fails is that, except at equilibrium, the angle of the arms is always lagging behind the speed of the flywheel, but that while it is lagging behind it is already being employed in regulating the steam valve. While there certainly is such a lag, it is not at all clear how this jeopardizes the claim that the angle arms are representations. Millikan, for example, contended that something could represent even if it never correlated with what it was to represent. The functional analysis of representations in terms of how components in the system use the representation was designed to allow for such mis-representation. Moreover, anyone who has advocated representations has recognized that when an effect represents its cause, there may be multiple steps in creating the representation, and so the representation may lag behind, and partly mis-represent the state being represented.
Finally, van Gelder offers what he takes to be the most compelling reason for rejecting representations: "The fourth, and deepest reason for supposing that the centrifugal governor is not representational is that, when we fully understand the relationship between engine speed and arm angle, we see that the notion of representation is just the wrong sort of conceptual tool to apply" (van Gelder, 1995, p. 353). What makes it the wrong sort of conceptual tool is that "arm angle and engine speed are at all times both determined by, and determining, each other's behavior" and this is a "much more subtle and complex relationship than the standard concept of representation can handle." While it may be more subtle and complex than some notions of representation can handle, it is not clear why it is too subtle and complex to satisfy the stand-in aspect of representation. Something can stand in for something else by being coupled to in a dynamical manner, and by being so coupled figure in determining a response that alters the very thing being represented.
None of van Gelder's arguments, therefore, suffice to demonstrate that the angle arms in the Watt governor do not stand in for the speed of the engine. Moreover, understanding how the Watt governor works seems to require this aspect of the notion of representation. Further, the fact that the representation is in a dynamical relation with what it represents (and with the user of the representation), does not undercut its status as a representation.
Although van Gelder focused his challenge to representations by focusing on the stand-in aspect, I suspect that what more frequently drives DST advocates opposition to representations is the fact that representations in DST systems are radically different in format from some others used in cognitive science, especially propositional representations. van Gelder and Port even suggest this themselves when they consider the possibility of finding representations in dynamical systems:
The larger point to be made, however, is that cognitive science has explored a wide variety of representational formats. DST, by introducing new notions such as trajectories and dynamic attractors, contributes to this ongoing exploration. One important contribution of DST is that it focuses on representations that change as the system evolves. This is an idea that has recently been developed in neuroscience as well; Merzenich and de Charms (1996), for example, emphasize how even the neurons that figure in a representation may change over time due to reorganizational processes in the brain. By providing tools for analyzing how representations may change dynamically, DST may make an important contribution to understanding representational format. In adopting this role, though, it is not challenging the use of representations but is a collaborator in understanding the format of representations.
The representations in the Watt governor and in visual systems such as the frog's retina are clearly very low-level representations. When cognitive theorists have appealed to representations, they have usually been focusing on much higher-level representations, for example, concepts that might designate objects in the world or linguistic symbols, figures and diagrams which we can use in reasoning and problem solving. Indeed, the notion of levels of representation has roots in a number of perspectives, including Donald's (1991) account of the evolution of mind, Halford's (1982) analysis of the ontogenesis of concepts in children, and Case's (1992) construal of the role of changes in frontal cortex during development. In another context, Clark and Karmiloff-Smith (1993) emphasize the importance of a process of representational redescription in which representations initially acquired in the performance of specific tasks (the sort of representations that might be encoded in the weights of connectionist networks) are redescribed so as to be available for other functions. A possible construal of van Gelder and other dynamicist's opposition to representations is that they are repudiating these higher order representations, not the more basic sensory representations on which I have been focusing.
This is not the context in which to mount an argument for higher-level representations. Others (e.g., Clark and Toribio, 1994) have argued that there are representation hungry contexts such as long-range planning and decision making, in which the objects and events with which a agent is coordinating its behavior are not present and for cognitive systems require such higher-level representations. Even if they are right, a useful contribution of dynamicists is to make us question, for any given explanation of behavior, whether such an appeal to higher-level representations is necessary. Many contexts thought to require higher-level representations may not in fact need them. My goal, however, has been simply to argue that the dynamicist's objections do not count against the need for low-level representations. Such low-level representations are important for cognitive science in at least two respects. First, just as in the case of the Watt governor, we need to appeal to such representations to understand how basic cognitive systems, such as the visual system, coordinate their behaviors with their environments. Second, if indeed cognition does require higher-level representations as well, the most plausible analysis is that such representations are built upon these low-level representations and perhaps inherit their content from them.
4. Two Models of Explanation
The focus on the role of representations in DST models has obscured a potentially more important aspect of some DST research that does set it apart from much other modeling in cognitive science. This is that it employs a very different model of explanation than that which underlies most modeling in cognitive science. Much of cognitive science research has been devoted to developing what Richardson and I call mechanistic explanation (Bechtel & Richardson, 1993). Mechanistic explanations differ significantly from a pattern of explanation much better known in philosophy of science, one involving derivations from covering laws. After identifying the differences between covering law and mechanistic explanations in the remainder of this section, I will argue in the next section both that some DST models are better construed as covering law explanations and examine how such explanations comport with mechanistic explanations sought by other cognitive scientists.
4.1 Covering Law Explanations
Until the last thirty years, philosophers of science focused primarily on physics as the prototypical science, especially areas in physics such as Newtonian mechanics and thermodynamics. From these disciplines, philosophers such as Rudolf Carnap, Ernest Nagel, and Carl Hempel extracted a model of explanation in which a phenomenon was explained by showing that it exemplified a basic law. This explanatory framework focused on the linguistic representation of the law and the phenomenon to be explained, and argued that a phenomenon was explained when a statement describing it was derived from statements specifying one or more laws and relevant initial conditions (Hempel, 1965). Thus, in explaining the temperature of a gas one might derive the statement specifying the temperature of the gas from a statement of Boyle's law that the temperature of a gas is proportional to the pressure times the volume and statements specifying the volume and pressure of the gas.
This understanding of explanation has its roots in Aristotle and, when it applies, is extremely intuitive. This is especially true if one considers not just static relations as in the above example, but dynamic ones by considering, for example, how the temperature would change if the pressure is increased but the volume is held constant. While the covering law model seems to fit some domains of science, even in these domains it raises some difficult questions. One such question is how one is to determine whether a true universal sentence, such as Boyle's law, is really a law or just an accidental truth. Hempel notes that one feature of a true law is that it supports counterfactuals, although this presents its own problem since, by definition, one can never test a counterfactual claim.
What has proven more problematic about the covering law model is that the laws of the sort needed for covering law explanations are not found frequently in the life sciences, including cognitive science. There are occasions when appeals to laws are made (e.g., to the Michaelis-Menten equation in biochemistry and to Shannon's laws of information in early cognitive psychology), but most research has a different objective than subsuming phenomena under universal laws. Instead, it is directed at revealing the particular processes at work in a given system (e.g., the particular substrates and enzymes involved in glycolysis or the particular operations performed in processing information).
4.2 Mechanistic Explanations
Following upon ideas developed by other philosophers focusing on biology (Wimsatt, 1980) and cognitive science (Cummins, 1983), Richardson and I presented mechanistic explanation as an alternative framework (Bechtel and Richardson, 1993). What is distinctive of mechanistic explanation is the appeal to the components of a system (described either physically or functionally) and their interactions.
Our interest was in the discovery of such explanatory accounts and we identify two heuristic assumptions adopted in pursuing such explanations, which we labeled decomposition and localization. Decomposition is the assumption that the overall activity results from the execution of component tasks. Localization is the assumption that there are components in the system that perform these tasks. The point of calling these heuristics is that they might prove to be false; they are important to the development of science because researchers proceed as if they were true. For example, biochemists proposed decompositions of a physiological process such as fermentation into a number of component reactions--reactions that were understood to be possible given purely chemical considerations--and then tried to localize these reactions by offering evidence that they actually transpired within living cells. This involved identifying intermediate substrates (e.g., by showing that they were present in trace amounts in normal cells and would accumulate when specific enzymes were inhibited) and demonstrating the existence of the enzymes which catalyzed each reaction (e.g., by showing that appropriate inhibitors could stop the reaction). Notice that localization need not involve actually identifying the enzymes, but may only involve the indirect demonstration that such enzymes performed the tasks proposed in the decomposition.
Decomposition and localization have been widely employed in the cognitive sciences. The attempt to decompose cognitive functions was certainly exemplified in the flow charts produced in early cognitive psychology (the legendary boxes in the head approach). Researchers tried to provide evidence for individual processes (boxes) by using behavioral measures such as reaction time: it was assumed that a task thought to involve additional operations beyond those used in another task would take correspondingly longer. Another way researchers tried to demonstrate the existence of a hypothesized process was to identify two tasks employing the same process: it was assumed that errors would result when a subject was required to perform both tasks simultaneously. A further source of evidence stems from deficit studies in neuropsychology. The strongest evidence, for neuropsychologists, involves discovering a double dissociation between two hypothesized cognitive processes, for example, between using a lexical process and a grapheme-to-phoneme transition rules to determine the pronunciations. By finding patients who exhibit deficits indicative of the failure of one of these processes but not the other, neuropsychologists offer evidence for the existence of separate processes (Shallice, 1988; for a critique see van Orden, Pennington, and Stone, in preparation).
This explanatory strategy is common not just in information processing psychology but in much of contemporary neuroscience; researchers try to decompose the tasks performed by the brain into component tasks and then seek evidence that these tasks are actually performed by neural components. Thus, Mishkin, Ungerleider, and Macko (1983) proposed a decomposition in visual processing into separate what and where processing systems and offered evidence based on lesion studies in monkeys that different neural systems were responsible for different types of processing. Subsequent research has proposed further decompositions in visual processing and tried to localize these in discrete brain regions (van Essen and DeYoe, 1995). Neuroimaging research, to give another example, uses techniques such as subtracting the activation patterns produced in one task from those produced in another, more comprehensive task to determine what brain areas figured in performing the additional parts of the task. These studies accordingly are seeking to identify hypothesized component psychological processes with specific brain regions.
5. Explanation in DST
Advocates of the DST approach, such as van Gelder, sometimes present DST as opposing the quest for such mechanistic explanations. To set up the contrast between DST explanations and more classical mechanistic explanations, van Gelder contrasts the Watt governor with a hypothetical computational governor, which might have been designed by decomposing the task of regulating the steam engine into a number of subtasks:
3. If there is no discrepancy, return to step 1. Otherwise,
a. measure the current steam pressure;
b. calculate the desired alteration in steam pressure;
c. calculate the necessary throttle valve adjustment.
4. Make the throttle valve adjustment.
Return to step 1. (van Gelder, 1995, p. 348)
van Gelder emphasizes that a computational governor built according to this decomposition would be homuncular (modular) in construction. He contends, moreover, that homuncularity is a property that has strong affinities with representation and other properties from which he seeks to distinguish DST accounts, such as computation and sequential and cyclic operation: "a device with any one of them will standardly possess others" (351).
van Gelder's suggestion is that the DST approach rejects the assumptions of decomposition and localization characteristic of mechanistic models. Some DST enthusiasts endorse a holistic perspective that is incompatible with mechanistic decomposition for the systems they analyze (van Ordan, et al.). Before accepting this opposition between DST and mechanism, we should examine mechanism more carefully. The above account of the computational governor is sequential and cyclic, but mechanistic explanations need not be. Early in the process of developing mechanistic models, scientists often assume that the processes that they are considering are performed serially. Richardson and I propose that the reason that scientists begin in this way has to do with the character of human cognition: our conscious reasoning tends to be linear and sequential. But, frequently nature is recalcitrant and it is not possible for scientists to develop a linear model that is adequate to the phenomenon. At this point scientists start to introduce feedback loops and other non-linearities in the attempt to develop adequate models. Such models, in which numerous components interact, sometimes in a manner that exhibits homeostasis, we call integrated systems. Such systems are not sequential and cyclic in van Gelder's sense.
The fermentation system is a good example. While earlier researchers sought to explain it in terms of a linear chain of reactions, and contemporary accounts still portray it in that way (Figure 3a), it is in fact a highly integrated system. The side loops in Figure 3a involve NAD and ATP, which integrate the various steps in the process by being produced in some reactions and consumed in other. If we change the diagram to show these coenzyme reactions as closed circles (Figure 3b),
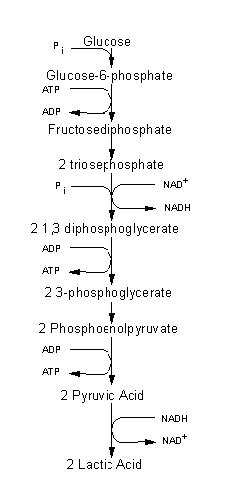
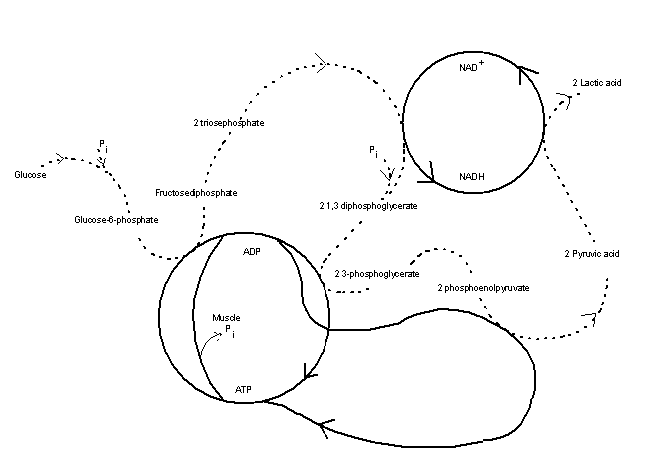
Figure 3. Two representations of the biochemical processes in fermentation.
(a) The common, linear representation, in which the reactions involving
the coenzymes are shown as side loops. (b) An alternative representation
in which the side loops are completed, revealing that the fermentation
system is an integrated system through which metabolites a processed.
this becomes apparent. There is certainly a componential or modular organization in the fermentation system. Moreover, as in many biochemical processes, researchers identify particular components in the system as carrying information about processes elsewhere in the system: the availability of ADP carries information that more energy is needed and that fermentation should continue, while the absence of ADP registers the fact that the system has all the energy it can consume. The system is so designed to then stop fermentation. But the fermentation system also exhibits a complex set of dynamical processes.
Thus, mechanistic explanations, pursued through the heuristics of decomposition and localization, are compatible with complex, integrated systems with non-linear dynamics. What makes these explanations mechanistic is that they still decompose the overall activity of the system into component activities and offer evidence that each of these activities is realized in the system. Thus, to return to the example of the Watt governor, while it does not employ the sequential and cyclic elements of the computational governor, it nonetheless can be given a mechanistic explanation: in explaining how it works, we identify three separate modules, each of which contributes something different to its operation (see Figure 2b). The components are tightly coupled with each other, but no more so than in the case of fermentation.
If even van Gelder's prototype of a dynamical system, Watt's governor, is amenable to mechanistic explanation, when does DST take us outside the domain of mechanistic explanation? Another distinction that van Gelder and Port (1995) draw reveals an important demarcation, but to set it up, we need to note one other distinction they make. While van Gelder and Port group many connectionists with more classical cognitive scientists, they allow that some connectionists are actually pursuing dynamical models. The distinction roughly is between connectionists who simply employ feedforward networks, which can be decomposed into sequential processing layers, and those who employ bi-directional interactions between nodes or recurrent connections. These networks constitute complex dynamical systems which may best be analyzed using tools from DST. van Gelder and Port (1995) speak of the connectionists who use DST tools for analyzing these more complex networks as "welcome participants in the dynamical approach" (p. 34). We will return to these connectionist models below, but now we can develop the distinction of interest. This is the distinction van Gelder and Port draw between connectionist and non-connectionist dynamical systems in terms of the fact that the connectionist models employ large numbers of components (units and connections), each engaged in the same type of activity, whereas non-connectionist DST models usually identify relatively few components which carry out quite different activities. A example of such a non-connectionist dynamical model is Townsend and Busemeyer's (1995) decision field theory. Their model consists of difference and differential equations relating parameters measuring the motivational value of consequences, attentional links between each consequence and each action, a valence or anticipated value of each action, a preference, and an actual behavior.
This division into qualitatively different components and specific relations between them might seem to show that DST accounts such as Townsend and Busemeyer's are examples of mechanistic explanations. This, however, misrepresents what these DST theorists are trying to do. The difference and differential equations in these models are intended to describe patterns of linked change in the values of specified parameters in the course of the system's evolution over time. The parameters do not correspond to components of the system which interact causally. They are, rather, features in the phenomenon itself (e.g., the motivational value a person assigns to a particular consequence).
What this reveals is that some DST accounts are better construed as characterizing the behavior or evolution of a system than as mechanistic explanations. In this respect, these DST explanations better fit the alternative, covering law model of explanation presented earlier. In order to distinguish explanations from descriptions, proponents of the covering law model argued that the generalization from which the behavior of the particular instance is to be derived really had to be a law. But it proved very difficult to specify just what made a universally quantified statement into a law. One of the agreed upon characteristics of a law, though, is that it supports counterfactuals. That is, a law would have to specify what would happen if the conditions specified in its antecedent were met. DST accounts, such as the one above, are clearly designed to support counterfactuals. They are designed to tell what would happen under different motivational values, for example. This suggests that it may be appropriate to construe these DST explanations as being in the covering law tradition.
Hence, the distinction van Gelder and Port drew between two sorts of DST explanations, connectionist and non-connectionist, represents a bigger gulf--that between mechanistic explanations and covering law explanations. Insofar as they are seeking a different kind of explanation, these DST theorists are genuinely doing something very different than those cognitive scientists who are seeking to understand the mechanisms of cognition. In this respect, it is appropriate to construe DST as revolutionary. (Some, however, might see is as more counterrevolutionary. In their quest for mechanistic explanations, early cognitivists such as George Miller and Gordon Bower differentiated their models from those of contemporary mathematical models, which, like contemporary DST models, proposed mathematical relations between parameters in the behavior of a psychological system.)
6. Relations between DST and Mechanistic Accounts
Following van Gelder and Port, I have distinguished two strands in contemporary DST research: connectionist and non-connectionist, and have gone on to argue that non-connectionist DST is revolutionary in adopting a different conception of explanation than the mechanistic conception adopted by most cognitive scientists. Having drawn that distinction, one can still ask how each form of DST relates to more traditional cognitive approaches.
In the case of non-connectionist DST theorists, the question is whether their explanatory pursuits are compatible with the search for mechanistic explanations. In many cases they are not only compatible, they complement that search. Assume that we have a correct DST account of motor behavior (e.g., as proposed in Kelso, 1995), of motor development (Thelen, 1995), of perception (Turvey and Carello, 1995), or of decision making (Townsend and Busemeyer, 1995). Each of these invites a further question: how is the underlying system able to instantiate the laws identified in these DST accounts? One way to answer this question is to pursue a mechanistic explanation by trying to decompose the overall behavior and localize subtasks. Even if we succeed in developing a mechanistic explanation, that explanation does not have greater priority. Nature is hierarchically organized, and for any system that is identified, different processes operate intrasystemically and intersystemically. If we want to characterize interactions between systems, we need to appeal to the processes operating at that level, not those operating intrasystemically. If a DST account provides an account at this level, its legitimacy is not undercut by learning how the various components in the system operate and perform their individual roles.
There is a further role, moreover, that DST accounts may play. Research efforts seeking to explain how a system does something which it does not in fact do may be wasted. To avoid this fate, it is helpful to have a good description of what a system is doing before trying to explain how it does it. My contention is similar to that of some advocates of ecological validity in cognitive research (e.g., Neisser, 1982) who argue that without attention to how cognitive processes operate in real settings, psychologists may be developing explanatory accounts of what are in fact laboratory artifacts. Neisser's use of the language of ecological validity is drawn from James Gibson, and it is noteworthy that several of today's DST theorists (Kelso, Turvey, and Shaw) are also neo-Gibsonians. Thus, one important contribution of DST accounts is to provide the most adequate characterization of the behavior of a cognitive system. These will be essential even for those embarked on identifying the underlying mechanisms.
Turning now to connectionist DST theorists, the question of how their models comport with mechanistic explanatory objectives does not arise, since connectionist models are models of mechanisms. The DST approach is employed by these theorists to analyze how these mechanisms behave. A good example arises in Elman's (1991) attempt to analyze simple recurrent networks which he uses to model a language related task of predicting each successive word in a corpus of sentences. The question motivating this research is whether recurrent connections provide sufficient information for the network to predict words of grammatically appropriate categories. Elman demonstrated that when an appropriate training regime was used the network's predictions would respect even fairly long range grammatical dependency relations. For example, the network would predict that the main verb in "boys who Mary chases feed cats" had to be plural.
Elman then raised the question of how the network was able to do this. Clearly a major part of what the network does is to create appropriate activation patterns on the hidden units. Given the number of hidden units (70) in his network and the fact that the hidden unit representations were likely to be very distributed, it was not feasible to analyze the network unit by unit (as, for example, Hinton (1986) was able to do). Accordingly, Elman has employed tools such as cluster analysis and principal components analysis. He employs principal components analysis to provide a reduced dimensional analysis of the representations on the hidden units. He is then able to show on which dimensions there is a difference between when the network is processing "boys hear boy" and "boy hears boys"; presumably it is these differences which account for the network's performance.
While Elman's network is more complex than many mechanistic systems, and accordingly more sophisticated tools are needed to analyze it, Elman is applying the heuristics of decomposition and localization to explain its performance. The task is decomposed, in part, by invoking a linguistic analysis according to which one task is to insure that the verb number agrees with that of the subject. Localization is not accomplished by finding a component responsible for insuring this agreement, because the information is distributed. But nonetheless, Elman is able to show that the relevant information is captured in the representations on the hidden units. It is noteworthy that in this explanation, Elman appeals to representations. Hidden units in recurrent networks, as in non-recurrent networks, represent aspects of the input, and he proposes to use tools such as principal components analysis to determine how. Such analyses in terms of representations are not at all surprising in mechanistic accounts, though, since what must be done in such accounts is to explain how information is carried through the system and made available to other parts of the system that use it.
7. Conclusion
In analyzing the revolutionary claims of some advocates of DST, I have focused on two features of the DST world view--the status of representations and the form of explanation employed. With respect to representations, I have distinguished the stand-in and format aspects of representations. Some DST advocates such as van Gelder have proposed that DST provides a way of doing away with representations in the stand-in sense, but I have argued against these claims. In understanding how the mind/brain carries out its tasks, we seek to identify how processes in it carry information about the world with which agents must deal, and how these processes figure in developing behavioral responses to the world. The essential notion I have been using here is a very minimal one, and one that admittedly makes representations fairly ubiquitous. They appear in any organized system which has evolved or been designed to coordinate its behavior with features of its environment. Thus, there are representations in the Watt governor, in biochemical systems, and in cognitive systems. But this notion is basically the same one invoked by both Newell in his classical account of physical symbol systems and by van Gelder in his attack on the need for representations.
Recognizing this may defuse the revolutionary character of DST. But it returns the focus to the other aspect of representation, the issue of format. Here DST provides additional alternatives to the major models of representational format considered so far in cognitive science, such as depictive versus propositional formats. These representations have often been static and one of the salutary contributions of DST is to focus attention on changing processes within a system that may serve to carry information needed by the system and hence constitute representations for it.
With respect to the type of explanation employed, I have argued that some DST accounts, those of non-connectionist DST modelers, do adopt a different model of explanation than that which has been characteristic of work in cognitive science. Most cognitive science research has been devoted to determining the nature of the mechanisms underlying cognitive performance, whereas some DST accounts are rather directed toward identifying laws that relate different parameters in a system. But while there is a difference here between DST accounts and other cognitive accounts, this does not render the two approaches incompatible. Indeed, they are complementary. We want to know both what the regularities are in the phenomena, and what mechanisms underlie them.
References
Anderson, J. R. (1983). The architecture of cognition. Cambridge, MA: Harvard University Press.
Anderson, J. R. (1990). The adaptive character of thought. Hillsdale, NJ: Lawrence Erlbaum Associates.
Ballard, D. H. (1991). Animate vision. Artificial Intelligence, 48, 57-86.
Bechtel, W. (1986). The nature of scientific integration. In W. Bechtel (ed.), Integrating scientific disciplines (pp. 3-52). Dordrecht: Martinus Nijhoff.
Bechtel, W. and Richardson, R. C. (1993). Discovering complexity: Decomposition and localization as strategies in scientific research. Princeton: Princeton University Press.
Case, R. (1992). The role of the frontal lobes in the regulation of cognitive development. Brain and Cognition, 20, 51-73.
Churchland, P. S., Ramachandran, V. S., and Sejnowski, T. J. (1994). A critique of pure vision. In C. Koch and J. L. Davis, Large-scale neuronal theories of the brain. Cambridge, MA: MIT Press.
Clark, A. (1996). Being there. Cambridge, MA: MIT Press.
Clark, A. (1997). The dynamical challenge. Cognitive Science, 21, 461-481.
Clark, A. and Karmiloff-Smith, A. (1993). The cognizer's innards: A psychological and philosophical perspective on the development of thought. Mind and Language, 8, 487-519.
Clark, A. and Torribio, J. (1993). Doing without representing? Synthese, 3, 401-431.
Cummins, R. (1983). The nature of psychological explanation. Cambridge, MA: MIT Press.
Donald, M. (1991). Origins of the modern mind: Three stages in the evolution of culture and cognition. Cambridge, MA: Harvard University Press.
Dretske, F. (1988). Explaining behavior: Reasons in a world of causes. Cambridge: MA: MIT Press.
Elman, J. (1991). Distributed representations, simple recurrent networks, and grammatical structure. Machine Learning, 7, 195-225.
Elman, J. (1995). Language as a dynamical system. In R. Port and T. van Gelder (eds.), Mind as motion. Cambridge, MA: MIT Press.
Fodor, J. A. (1980). Methodological solipsism considered as a research strategy in cognitive psychology. Behavioral and Brain Sciences, 3, 63-109
Fodor, J. A. and Pylyshyn, Z. (1988). Connectionism and cognitive architecture: A critical analysis. Cognition, 28, 3-71.
Grush, R. (1997). The architecture of representation. Philosophical Psychology, 10, 5-24.
Hatfield, G. (1990). Gibsonian representations and connectionst symbol processing: Prospects for unification. Psychological Research, 52, 243-252.
Haugeland, J. (1991). Representational genera. In W. Ramsey, S. P. Stich, and D. E. Rumelhart (eds.), Philosophy and connectionist theory (pp. 61-89). Hillsdale, NJ: Lawrence Erlbaum.
Hempel, C. G. (1965). Aspects of scientific explanation and other essays in the philosophy of science. New York: Macmillan.
Hinton, G. E. (1986). Learning distributed representations of concepts. Proceedings of the 8th Annual Conference of the Cognitive Science Society, pp. 26-33.
Halford, G. S. (1982). The development of thought. Hillsdale, NJ: Lawrence Erlbaum Associates.
Kelso, J. A. S. (1995). Dynamic patterns: The self organization of brain and behavior. Cambridge, MA: MIT Press.
Kosslyn, S. M. (1980). Image and Mind. Cambridge, MA: Harvard University Press.
Kosslyn, S. M. (1994). Image and brain: The resolution of the imagery debate. Cambridge, MA: MIT Press.
Lettvin, J. Y., Maturana, H. R., McCulloch, W. S. and Pitts, W. H. (1959). What the frog's eye tells the frog's brain. Proceedings of the IRE, 47, 1940-51.
Merzenich, M. M. and de Charms, R. C. (1996). Neural representation, experience, and change. In R. Llinás and P. S. Churchland (eds.), The mind-brain continuum. Cambridge, MA: MIT Press.
Millikan, R. (1984). Language, thought, and other biological categories. Cambridge, MA: MIT Press.
Millikan, R. (1993). White queen psychology and other essays for Alice. Cambridge, MA: MIT Press.
Minsky, M. (1975). A framework for representing knowledge. In P. H. Winston (ed.), The psychology of computer vision, pp. 211-79. New York: McGraw Hill.
Mishkin, M., Ungerleider, L. G., and Macko, K. A. (1983), Object vision and spatial vision: Two cortical pathways. Trends in Neuroscience, 6, 414-417.
Neisser, U. (1982). Memory observed. San Francisco: Freeman.
Newell, A. (1980). Physical symbol systems. Cognitive Science, 4, 135-183
Pollack, J. (1990). Recursive distributed representations. Artificial Intelligence, 46, 77-105.
Pylyshyn, Z. W. (1973). What the mind's eye tells the mind's brain: A critique of mental imagery. Psychological Bulletin, 80, 1-24.
Pylyshyn, Z. W. (1981). The imagery debate: Analogue media versus tacit knowledge. Psychological Review, 87, 16-45.
Schank, R. C. and Abelson, R. P. (1977). Scripts, plans, goals and understanding. Hillsdale, NJ: Erlbaum.
Shallice, T. (1988). From neuropsychology to mental structure. Cambridge: Cambridge University Press.
Smolensky, P. (1990). Tensor product variable binding and the representation of symbolic structures in connectionist systems. Artificial Intelligence, 46, 159-216.
Thelen, E. (1995). Time-scale dynamics and the development of an embodied cognition. In R. Port and T. van Gelder (eds.), Mind as motion. Cambridge, MA: MIT Press.
Townsend, J. T. & Busemeyer, J. (1995). Dynamic representation of decision-making. In R. Port and T. van Gelder (eds.), Mind as motion. Cambridge, MA: MIT Press.
Turvey, M. T. and Carello, C. (1995). Some dynamical themes in perception and action. In R. Port and T. van Gelder (eds.), Mind as motion. Cambridge, MA: MIT Press.
van Essen, D. C. and DeYoe, E. A. (1995). Concurrent processing in the primate visual cortex. In M. S. Gazzaniga (Ed.).
van Gelder, T. (1990). Compositionality: A connectionist variation on a classical theme. Cognitive Science, 14, 355-384.
van Gelder, T. (1995). What might cognition be, if not computation? The Journal of Philosophy, 92, 345-381.
van Gelder, T. and Port, R. (1995). It's about time: An overview of the dynamical approach to cognition. In R. Port and T. van Gelder (eds.), Mind as motion. Cambridge, MA: MIT Press.
van Orden, C. G., Pennington, B. F., and Stone, G. O. (in preparation). What do double dissociations prove? Inductive methods and theory in psychology.
Wimsatt,W.C. (1972). Teleology and the logical structure of function statements. Studies in the History and Philosophy of Science, 3, 1-80.
Wimsatt, W. C. (1980). Reductionistic research strategies and their
biases in the units of selection controversy. In T. Nickles (Ed.), Scientific
discovery: Case studies (pp. 213-259). Dordrecht: Reidel